一、原始观念
兹举四个原始观念如下:
1.二分观念:我们现在以二分逻辑为标准逻辑,所以在讲推理系统时,不能不以二分观念为原始观念。二分是「是」与「不是」的二分,不关乎名称、类、或对象方面;它是思想方面的东西。
2.同一观念:这个观念普通名之曰思想律,在此不把它看成是律,而认它是原始观念。同一就是关于「是」的一致的肯定,也是思想方面的,不关于外界或对象方面。我们说话之所以有意义,同一是一个必须的条件。一个思想所以能成系统,前后一致,也完全靠同一观念。所以同一是说话有意义与否的关键,不关于对象的变与不变。
3.拒中观念:拒中观念是由二分观念而来的。既然是二分,便不能有中间存在。所以拒中则表示一定「是」或「不是」,决不允许:既是「是」又是「不是」,既不是「是」又不是「不是」。如是,拒中也函有同一在内。故拒中也是思想方面的,不关于对象。对象方面既无所谓二分,又无所谓拒中。但在思想的运行上,一定要有这个观念,不然便不能进行。拒中普通亦名之曰思想律,在此则名之曰原始观念。
4.矛盾观念:矛盾是拒中的另一种表示,是容中的禁止的表示。它一方面证成同一,一方面证成拒中。当然也是由二分观念而来的。它是「既是『是』又是『不是』」的禁止,它禁止「是」与「不是」同时主张。这也是思想方面的,不关于对象。对象无所谓矛盾。矛盾是两个命题的矛盾,矛盾观念即是要禁止矛盾的命题;若无这个观念,思想必不能进行,必无结论。所以在思想的运行上,一定要有矛盾观念。矛盾普通也名之曰思想律,在此则名之曰原始观念。
这四个原始观念就是使推演系统成为可能成为有意义的必须而且充足的条件。所谓必须,是说没有它便不行;所谓充足,是说有了它便行,用不着其它条件。
如果把这四个观念当作原则看,则一切推演都当遵守这四个原则。所推出的命题是否能成立,只要看它是否能合乎这四个原则。如果为这四个原则所允许,它便可以成立,否则便不能成立,如传统逻辑中所设立的许多禁律都是不必须的。
二、四种命题的说法
传统逻辑中AEIO四种命题,不是原子命题,乃是遍举命题。因为他们含有「一切」、「某些」两个观念。「一切」与「某些」在此都不牵涉到存在问题, 只是思想上的两个观念而已。「一切」是全举,「某些」是分举。「一切」固是抽象,无所指示;「某些」也是抽象,无所指示。因为所谓某些并不是特定的某些,是乃任何「某些」,所以便与外界无关。
普通讲命题,有说是主谓关系,有说是分子关系,有说是本体属性,有说是类与分子。在此都不计较,我们只注意是与不是的关系。因为逻辑只讲空架子,不问实际;只讲理,不讲物。如果空架子的理弄得一致无矛盾,便算尽职。至于如何应用架子,材料如何填进架子,那是认识问题。经验问题,不是逻辑所有事。逻辑只摆出理则而已。所以无论分子或主谓皆不重要。如果是分子,便当只以分子表示一致无矛盾的理则,主谓亦然。而一致无矛盾的理则只是是与不是间的推演关系。所以我们现在只注意是与不是的一致无矛盾。固然,普通以是与不是为主谓命题式,但此处所谓是与不是乃是一般的、二分法上的;如果主谓命题能表示是与不是的关系,我们就用这种命题也不妨。
如是,AEIO的说法如下:
A:一切S是P;
E:一切S不是P(不当说无S是P);
I :某些S是P;
O:某些S不是P。
如是,这种说法完全是是与不是,肯定与否定的表示。以后,换质换位中的一切肯定与否定,都当遵守这种说法。但是一般讲逻辑的人常不遵守,所以便有问题发生。
三、周延与量化
周延与不周延其实即是有漏无漏。有漏者为不周延,无漏者为周延。有漏亦即不穷尽,无漏即穷尽。穷尽即全举,不穷尽即分举。所以周延与不周延亦即全举与分举之意。一切S是P,此时S便是全举、周延、无漏;某些S不是P,此时S便是分举、不周延、有漏。
一切S是P,于換位时,为某些P是S。所以在传统逻辑中,便以P为不周延。即「一切S是P」中的P是分举,有漏的。因为「一切人是动物」,但动物却不都是人,所以在那个命中,宾词动物是不穷尽的、有漏的。同理,某些S是P,P也是不周延的。
但否定命题却有点不同。一切S不是P,在传统逻辑中,S固是周延,P也是周延。因为在他们看起来,一切S既不是P,则S便与P脱离了关系,既脱离了关系,则S是一个自足的全举,P也是一个自足的全举,两个全举互不相属,所以都可穷尽而无漏。同理,某些S不是P,S不周延,P却是周延。因为P与某部分S脱离了关系,则P与S不相属,自可自成一穷尽而无漏之全举。
如是,在传统逻辑中,AEIO的周延与否如下:
A命题:主词周延,宾词不周延;
E命题:主词周延,宾词周延;
I命题:主、宾词俱不周延;
O命题:主词不周延,宾词周延。
我们将见周延与否是传统逻辑中推理上一个重要禁律。因这个禁律的阻碍,直接推理事实上可以进行倒变成不能进行的了。在间接推理中,周延与否的禁律成了一个十分死记的东西,甚不一见即明;但是一个直接推理是否能成立,我们的直觉却很能使我们一见即明。所以周延与否的禁律,在推理中,实在是不必要的。传统逻辑中所以需要那种禁律,实在因为一个命题没有说清楚。如果说清楚了,其间的关系都是必然,结论自然流出。用不着当中横插许多不必须的禁律。
如是,我们不用周延与否当作禁律,我们把它说在一个命题里面,使着该命题较为严格。这样,命题间的推理便都是先验的、必然的,赤裸裸是命题间的关系,可以自由引申,而用不着禁律来限制。如是,AEIO可重说如下:
A命题:一切S是P→一切S是一切P→一切S是某些P;
E命题:一切S不是P→一切S不是一切p→一切S不是某些P(一切S不是一切P,不当说是不是任何P,「任何」的观念是不必须的,不当参加在内);
I命题:某些S是P→某些S是一切P→某些S是某些P;
O命题:某些S不是P→某些S不是一切P→某些S不是某些P(不是一切P,仍不当说不是任何P)。
这种主宾词都加上「一切」与「某些」的观念,便是命题的严格说法。有了这种说法,周延与否的禁律便用不着,因为一切结论都可从那些严格命题中引申出,周延或不周延都明白地表示出,都呈现在那命题上,所以便用不着它作禁律。
在宾词上加「一切」与「某些」的观念,是威廉·罕密儿顿(Sir William Hamilton)发明的。他叫它是宾词的量化,成为八个命题,于AEIO而外,又各与以专名。我以为这是不必须的。其实仍是四个命题,肯定与否定的性质并未变更,只不过把隐藏的弄明显罢了。有人以为这种量化很成问题,加以反对。其实也不必须。因为「一切S是P」,在換位时,成为「某些P是S」,这已显然把P量化了。因为已经预定量化,但未说出来,所以才有周延与否的禁律出现。现在把已经预定的说出来,取消周延的禁律,有何不可?有何问题?因为这是已经显然的事情了。并且「一切」与「某些」两观念并无理由不许加在宾词上。逻辑即是藉命题间的关系以表达理则。传统逻辑家专在那些不相干的问题上争论,结果是既繁杂又琐碎。而把逻辑又混同于方法论、工具学、认识论,这是最碍事的地方。
主宾词都加「一切」与「某些」来限制,则传统逻辑AEIO周延与否的格式便用不着。他们说:「一切S不是P」,其中P是周延的,但我们也可以看它是不周延的。因为「一切S不是某些P」,总是可以成立的,我们没有理由否认它。他们所以肯定地说它是周延的,实在是吃了圆圈的亏。他们用圆圈把E命题表示如下:
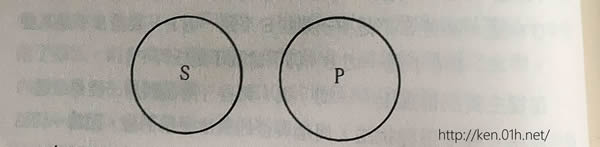
在此图中,S与P两不相属,所以S是自足的全举,P也是自足的全举。但是P为何必是全举?虽然圆圈是整个的,但是分举又何尝不在几何空间上占一地位,这一地位又何尝不可以圆圈表之?所以P必是周延的肯定不是必然的。圆圈的表示最好不用,唯一当遵守的原则是矛盾的原则。
四、AEIO的四角关系
传统逻辑讲AEIO的关系也是十分不严格的。他们叫A与E间的关系是反对关系(contrary relation),此名甚不恰。反对亦即相反,然而是与不是明明是矛盾关系,如何能是相反?须知相反与矛盾不同。相反者未必矛盾,然矛盾必相反;相反者可以是对象,然矛盾必是命题;相反可以并存,然矛盾不能并存;相反可以是两物之存在,然矛盾则是两命题之真假,不关系存在。譬如红色与白色可以并存,但这是红的,与这不是红的,这两个命题不能同时为真。如果同时说,便等于自己打自己嘴,便等于无说,算是个零。此即所谓矛盾关系。但相反并不如此。相反可以是一,也可以是二。红绿相化成紫这是一,红花绿叶这是二,然都可以相反而并存。「这是红的」与「这是绿的」可以并存,但「这是红的」与「这不是红的」不能同真。是红与不是红是陈说的一个对象,这两个命题不能并真;是红与是绿是陈说的两个对象,在命题方面可以并真,在对象方面可以并存。不能并真为矛盾,可以并真并存是相反。如是,是与不是为矛盾,既是又是为相反。是红与不是红为矛盾,是红与是绿是相反。A与E乃是是与不是的形式,不是既是又是的形式。故知A与E的关系是矛盾关系,不是反对关系。
他们又说反对关系的条件如下:
㈠可以同时假;
㈡不能同时真;
㈢由一命题之真可以推论到第二命题之假;
㈣由一命题之假不能推论到第二命题之真或假。
这四个条件是A与E间所具有的,所以他们是反对关系。其实按矛盾关系说,第一条件与第四条件不能成立。他们解说可以同时假如下:一切S是P,一切S不是P,只要有一部份S是P,则一切S不是P是假,只要有一部份S不是P,则一切S是P是假。所以A与E可以同时假。这个解说实在可笑,逻辑家不应有此!既然肯定了一切S是P,怎样又可以假设一部份S不是P?这根本犯了矛盾关系。我们讲的是A与E的关系,不是A包着O,E包着I的关系。也许他们以为:一切S是P,是一个假设,若事实上不是一切S是P,则一切S是P岂不是假?但逻辑实在是只讲随着假设而有的结论,不关乎实际上是否是P。既假设而肯定之,复假设而否定之,这简直是开玩笑!哪里是讲逻辑?同理,既然肯定了一切S不是P,便不应假设一部分S是P以否定之。所以「可以同时假」这个条件决定是不能成立的。既不能同时假,则第四条件也不能成立。第四条件是说:由一命题之假不能推论到第二命题之真或假。他们解说道:既可以同时假,又不同时真。则A是假的,E可真可假;E是假的,A可真可假。这些解说都是不可思议,根本违犯二分、同一、拒中、矛盾诸原则。他们所以不对,也是吃了圆圈的亏。他们用圆圈表示AE关系如下:
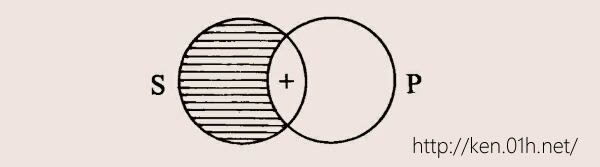
+号表示真,横线处表示假。有+号处为一切S是P,有横线处为一切S不是P。如果一切S是P为真,一切S不是P便假。这是不同时真的表示。其它AE间的真假关系也同样用圆圈表示。但须知用圆圈表示也罢,惟用那样画法的圆圈表示则大不对。A命题是一切S是P,既然一切S是P,怎么会有一部份S不是P、在P外?既然一切S是P,怎么成了一部份S是P,即一部份S在P内?这都是开玩笑,不可思议。即使用圆圈表示也当如下:
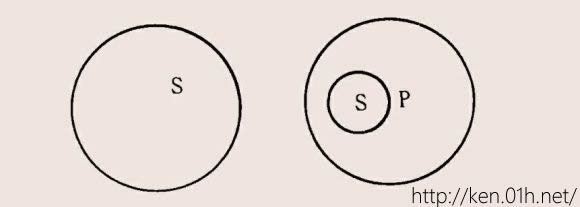
这样表示便是㈠一切S是P为真,一切S不是P便假;㈡一切S不是P为真,一切S是P便假;㈢不能同时真;㈣不能同时假。这样,才能恰合AE的性质的关系。也许他们以为这样表示,不能达出他们所谓反对关系,所以用另一种画法。但须知那种画法根本抵触了AE两命题的性质,根本否认了AE两命题,所以圆圈的表示适足害事。
因此,我们说AE间的关系是矛盾关系。因为肯定与否定,是与不是,根本矛盾故,非相反故。其情形如下:
㈠不能同时真;
㈡不能同时假;
㈢由一命题之真可以推到第二命题之假;
㈣由一命题之假可以推到第二命题之真。
这样便恰合AE的性质,又恰合矛盾原则。若把A命题限为「一切S是某些P」,E命题限为「一切S不是某些P」,其间的关系也是矛盾的。因为这仍是「是」与「不是」的形式。此其一。A命题只指出某些P,于某些P而外并未指出其它,所以一切S只与它所指出的某些P发生确定关系,并未与某些P而外的未指出的东西发生关系。既然如此,则E命题所否定的也只能是A命题所指出的,并不能否定或肯定A所指出的某些P而外的东西。所以一切S是某些P,并未预定一切S是或不是某些P而外的另一些P;而一切S不是某些P,也并未预定一切S是或不是它所否定的某些P而外的另一些P。这意思是说:A命题中的「某些」与E命题中「某些」同一。所以如果AE中的「某些」是同一的,则AE便矛盾。表示这种同一,最好以指示形容词「这个」或「此」加之。如是,A命题可以写为:「一切S是此某些P」,而E命题则为:「一切S不是此某些P」。不过,如果在「某些」上没这种限制,在AE命题上也不会有歧义。此其二。所以AE两命题,其宾词无论如何限制,总是矛盾的,没有歧义。
但是,I与O稍繁杂一点。I命题为「某些S是P」,O命题为「某些S不是P」。这两个主词的「某些」若是同一的,无论宾词如何限制,总是矛盾的。表示这种同一,仍以「此」加之。如是,「此某些S是P」、「此某些S不是P」是矛盾的。如果主词「某些」不是同一,没有限制,则某些S是P,某些S也可以不是P,IO两命题便可以相容、不矛盾。「某些」在主词有歧义,「某些」在宾词无歧义。其所以然之故,即在:在宾词有是与不是的矛盾以限之,在主词则暗含既是又是的相反并存而并不矛盾。
如是,肯定与否定可以相反并存者曰相容,相反而不可以并存者曰矛盾。AE为全矛盾,IO可为矛盾,可为相容。在传统逻辑,叫IO为下反对关系(subcontrary),也是不对的。如是,IO的情形如下:
1. 若主词「某些」相同一,则矛盾,真假关系同AE。
2. 若主词「某些」不同一,则相容,真假关系为并存:
㈠可以同真;
㈡不能同假;
㈢I真,O可以假,IO不相干(不是由I真可以推O假);
㈣I假,O可以真,IO不相干(不是由I假可以推O真)。
再论AO与EI的关系。此两关系比较更复杂。传统逻辑名之曰矛盾关系。其实也不然。因为它们没有AE的情形。A说「一切S是P」,O说「某些S不是P」。这是否定了一切S的一部,既否定了一部,一切便不能成立。所以O真A便假。O若假,即表明有些S可以是P,但却并不能说一切S是P。所以O若假,A可真可假,真假不定,这即由部份不能推全体之意。即此一点,已足证明AO不是矛盾关系。从A方面着想,情形却不同。A真,O假;A假,O真。从A到O是矛盾的,从O到A不是矛盾的。两不相称。其关系如下:
㈠A真,O假;
㈡A假,O真;
㈢O真,A假;
㈣O假,A或真或假。
此关系可以叫做半矛盾关系,而其特殊情形,由第四条可以暗示出:
㈠OA可以同假(不是必同假);
㈡OA决不能同真。
按此特殊情形,可以把半矛盾取消,名之曰「不相容」。
AO如此,EI也是如此。先从E方面着想:「一切S不是P」若真,则「某些S是P」必假;「一切S不是P」若假,则「某些S是P」必真。但从I方面着想,便不如此。「某些S是P」若真,则「一切S不是P」便假;「某些S是P」若假,则「一切S不是P」可真可假,真假不定,这也是由部份不能推全体之意。如是:
㈠E真,I假;
㈡E假,I真;
㈢I真,E假;
㈣I假,E或真或假。
由第四条,其特殊情形:
㈠IE可以同假(不必同假);
㈡IE决不能同真。
此与AO同,也可名之曰「不相容」。这种关系,宾词用不着加限制,「某些」也用不着加限制。
再论AI与EO。此两关系,在传统逻辑名曰差等,此没有什么错处,因同质故。A为「一切S是P」,I为「某些S是P」。A真,I亦真;A假,I亦假。但是,I真,A或真或假,真假不定;I假,A亦假。E为「一切S不是P」,O为「某些S不是P」。如是,E真,O真;E假,O假。但是,O真,E不定;O假,E假。如是,AI关系如下:
㈠可以同真;
㈡可以同假;
㈢I真,A不定。
EO的关系如下:
㈠可以同真;
㈡可以同假;
㈢O真,E不定。
在这两对关系上,有一种特殊情形,即OI真,AE不定,但AE真,OI却必有定。如是,从AE到IO方面说,AE或真或假,IO必真,这个情形便有似于算理系统的真妄含蕴(material implication)关系。所以这两对关系,在普通名曰「差等」,此处可与以专名曰「含蕴」,即A含蕴I,E含蕴O。所谓含蕴,是被含蕴者的真妄定值多,含蕴者的真妄定值少之谓。含蕴者的真妄定值所以少,即因为它的外范大。所谓差等,也就是AE的外范大,IO的外范小,所以IO随同AE连带其真妄,但AE却不能随同IO连带其真妄,AE不能随同IO即表示其真妄定值少于IO,所以AE含蕴IO。
以上AE;IO;AO,EI;AI,EO四种关系,其真妄值可以格式表之如下。
㈠AE的关系是「矛盾」(A≈E):
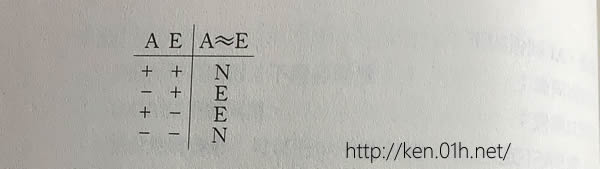
+号表非真,-号表非假。N表示不成立或不存在,E表示成立或存在。
㈡IO的关系是「相容」(I∨O)(「某些」不加限制):

「某些」若加限制便是矛盾如下:

㈢AO与EI两者的关系是「不相容」(A︱O,E︱I):
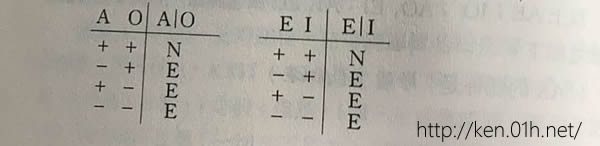
㈣AI与EO,两者的关系是「含蕴」(A⊃I,E⊃O):
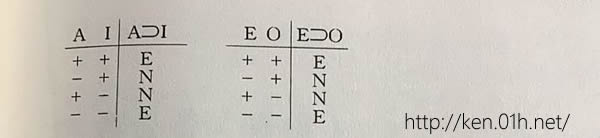
如是,这四种关系可以四角图表之如下:

此关系图既简易,又均称,复恰合各命题之性质,也用不着许多限制与补充。以往诸解法俱入魔道。愈修改,愈繁难,愈不通。此关系图只遵守第一段所述的那四个原则,其余皆不必须,而亦无不圆融一贯。至于金岳霖先生对于AEIO的三种看法,我以为是自作陷阱,自入火坑,自出火坑,乃是用不着的麻烦。盖逻辑决不许如此牵涉也。
本文当与本刊17期〈逻辑当以命题表达理则为对象〉及19期〈论逻辑中之二分法〉两文合观。
原载《民国日报•哲学周刊》第20/21期 1936年1月15/22日